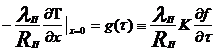 (13)
(13)
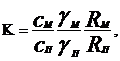 Где
Где
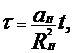
![]()
Подставляя значение ![]() из условия (2) в решение задачи Коши (3) получим
из условия (2) в решение задачи Коши (3) получим
![]() (14)
(14)
где
![]()
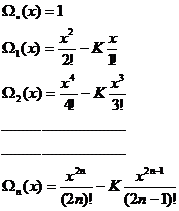
Таким образом, решение этой задачи имеет вид
![]() (15)
(15)
где ![]() нам задана, а функции
нам задана, а функции ![]() (n=1, 2, … , N) определяются из решения интегральных уравнений Вольтерра первого рода (5) методом регуляризации
(n=1, 2, … , N) определяются из решения интегральных уравнений Вольтерра первого рода (5) методом регуляризации
(7) - (9).
Следовательно, искомые величины![]()
![]() определяются из решения (4) с использованием регуляризирующего алгоритма (7) - (9).
определяются из решения (4) с использованием регуляризирующего алгоритма (7) - (9).
Метод наименьших квадратов.
Пусть функция ![]() задана на
задана на ![]() своими значениями в точках
своими значениями в точках ![]() . Рассмотрим совокупность функций
. Рассмотрим совокупность функций
![]()
![]() (16)
(16)
линейно независимых на ![]() .
.
Будем отыскивать линейную комбинацию этих функций
![]() (17)
(17)
так, чтобы сумма квадратов ее отклонений от заданных значений ![]() функции в узлах
функции в узлах ![]() имела бы наименьшее возможное значение, то есть величина
имела бы наименьшее возможное значение, то есть величина
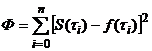 (18)
(18)
принимала бы минимальное значение.
Заметим, что упомянутая сумма является функцией коэффициентов
![]() . (19)
. (19)
Поэтому для решения нашей задачи воспользуемся известным приемом дифференциального исчисления, а именно: найдем частные производные функции ![]() по всем переменным и приравняем их нулю:
по всем переменным и приравняем их нулю:
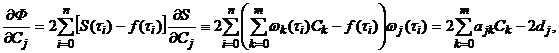
где
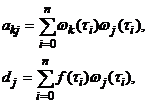
Отсюда видим, что метод наименьших квадратов приводит к необходимости решать систему алгебраических уравнений

![]() . (20)
. (20)
Можно доказать, что если среди точек ![]() нет совпадающих и
нет совпадающих и ![]() , то определитель системы (20) отличен от нуля и, следовательно, эта система имеет единственное решение (19). Подставив его в (17), найдем искомый обобщенный многочлен
, то определитель системы (20) отличен от нуля и, следовательно, эта система имеет единственное решение (19). Подставив его в (17), найдем искомый обобщенный многочлен ![]() , те есть многочлен, обладающий минимальным квадратичным отклонением
, те есть многочлен, обладающий минимальным квадратичным отклонением ![]() . Заметим, что при m = n коэффициенты (19) можно определить из условий
. Заметим, что при m = n коэффициенты (19) можно определить из условий ![]()
![]() причем в этом случае Ф = 0. Следовательно, мы приходим здесь к рассмотренной ранее задаче интерполирования.
причем в этом случае Ф = 0. Следовательно, мы приходим здесь к рассмотренной ранее задаче интерполирования.
 Вблизи поверхности Земли ускорение свободного падения зависит ОТ широты местности. Это объясняется нешарообразностью формы Земли и влиянием суточного вращения Земли вокруг своей оси.
Вблизи поверхности Земли ускорение свободного падения зависит ОТ широты местности. Это объясняется нешарообразностью формы Земли и влиянием суточного вращения Земли вокруг своей оси.
 Законы физики основаны на фактах, установленных опытным путем.
Законы физики основаны на фактах, установленных опытным путем.
 Турбина 16 века использовавшая энергию движущейся воды, применялась для привода ирригационных насосов.
Турбина 16 века использовавшая энергию движущейся воды, применялась для привода ирригационных насосов.