где - безразмерные время и координата.

Нетрудно убедиться, что решение задачи (1), (2), записанное в виде:

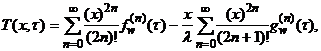(3)

и является искомым /10/.

Утверждения о существовании решения (3), об аналитичности этого решения и его единственности в классе аналитических функций составляют содержание известной классической теоремы Коши - Ковалевской /11/.

Решение (13) при заданных и позволяет найти искомые изменения температуры и теплового потока Однако в такой интерпретации решения (3), где функции известны из эксперимента с некоторой заданной погрешностью, необходимо учитывать и тот факт, что вычисление операторов дифференцирования неустойчиво к возмущениям в исходных данных /12/.

Таким образом, имеем типичную некорректную задачу, для построения устойчивого решения которой необходимо построение регуляризирующих алгоритмов.

Сохраним в решении (3) конечное число слагаемых N. Введем обозначения

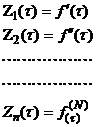(4)

Интегрируя (4) получим систему интегральных уравнений Вольтерра первого рода:

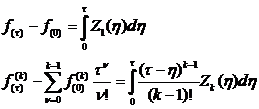, (5)

где k =1, 2, . , N.

Соотношения для теплового потока в (3) записывается аналогично. В дальнейшем будем считать, что на поверхности X = 0 теплосъем отсутствует, то есть стенка теплоизолирована. Тогда решение (3) с учетом обозначений (4) записывается в виде

(6)

Таким образом, граничные условия при X = 1 восстанавливаются соотношением (6), в котором функции находятся из решения интегральных уравнений (5)

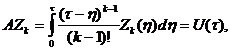(7)