При решении задач электродинамики, учитывается, что все макроскопические тела ограничены поверхностями. При переходе через эти поверхности физические свойства макроскопических тел изменяются скачком и поэтому также скачком могут изменяться электромагнитные поля, создаваемые этими телами. Другими словами векторные функции и являются кусочно-непрерывными функциями координат, т.е. они непрерывны вместе со своими производными внутри каждой однородной области, но могут претерпевать разрывы на границах раздела двух сред. В связи с этим представляется удобным решать уравнения Максвелла (1) - (4) в каждой области, ограниченной некоторой поверхностью раздела отдельно, а затем полученные решения объединять с помощью граничных условий.

При нахождении граничных условий удобно исходить из интегральной формы уравнений аксвелла. Согласно уравнению (4) и теореме Остроградского-Гаусса:

, (16)

где Q – полный заряд внутри объёма интегрирования.

Рассмотрим бесконечно малый объём в виде цилиндра с высотой h и площадью основания S, расположенный в средах 1 и 2 (рис. 2).

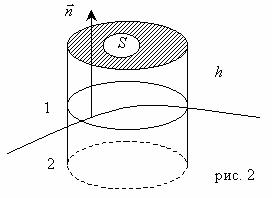Соотношение (16) в этом случае можно записать виде:

(17)

здесь - нормаль к границе раздела двух сред, направленная из среды 2 в среду 1. Знак «минус» во втором слагаемом обусловлен тем, что внешняя нормаль поверхности интегрирования в среде 2 направлена противоположно нормали в среде 1. Пусть основание цилиндра стремится к границе раздела двух сред. Так как площадь боковой стремится к нулю, то , и поэтому (17) приобретёт вид:

(18)

где и - значения нормальных составляющих вектора по разные стороны поверхности раздела; - поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества. Если поверхность раздела не заряжена, то в формуле (18) необходимо положить =0. Пользоваться понятием поверхностной плотности удобно тогда, когда избыточные (сторонние) заряды расположены в очень тонком слое вещества d, а поле рассматривается на расстояниях от поверхности r>>d. Тогда из определения объёмной плотности заряда следует:

= d = .

Если учесть, что , а - поверхностная плотность поляризационных зарядов, то формулу (18) можно записать в виде:

где , а величина , которая входит в граничное условие (18), есть поверхностная плотность зарядов, избыточных по отношению к связанным зарядам самого вещества.

Используя уравнение (2) и проводя аналогичные рассуждения, получаем граничное условие для вектора :

(19)

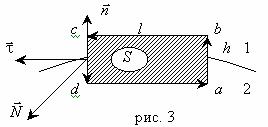
Выражения (18) и (19) – граничные условия для нормальных составляющих векторов и . Чтобы получить условия для тангенциальных составляющих можно использовать уравнения (1) и (3). Умножим уравнение (3) скалярно на положительную нормаль к поверхности S, ограниченной контуром L, имеющим вид прямоугольника (рис. 3).